モデルの説明
植物(主に葉の繁った樹木)が伝搬路に存在する場合、伝搬損失が発生する。森林では地上パスと上空から到来する電波(スラントパス)の伝搬損失モデルがある。どちらのモデルも樹木帯の経路長(森林の通過距離)と周波数に応じて伝搬損失量が変化する。また、様々なエリアでの実験結果に基づき、木の種類による特性の変化を、これに関係する係数を用いて表している。

森林では下記のように地上パスと上空から到来する電波(スラントパス)の伝搬損失モデルがある。
【森林:地上パス】
\(
A_{ev}=A_m[1-\exp(-d\gamma/A_m)]
\tag{1}
\)
\(
A_m=A_1\cdot f^{α}
\tag{2}
\)
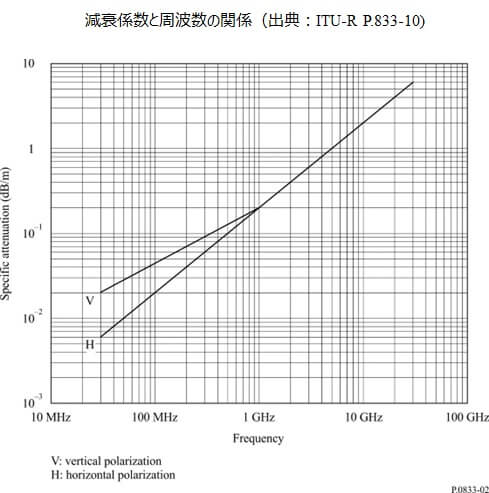
ただし,\(\gamma\)は周波数により変化する。ITU-R P.833-10には周波数と\(\gamma\)の関係がグラフ(下図)で示されている。\(α\)、\(A_1\)は木の種類と周波数により異なることが様々なエリアの測定で確認されている。
【森林:上空から到来する電波(スラントパス)】
上空から到来する電波の植生損失は仰角\(θ\)を導入して次式で計算される。
\(
L = A\cdot f^B\cdot d^C\cdot (θ+E)^G
\tag{3}
\)
ただし,\(A、B、C、E、G\)は木の種類に関係する係数である。
パラメータ
各推定式の係数の代表値は以下のとおりである。
【森林:地上パス】 【森林:上空から到来する電波(スラントパス)】
| 係数 | リオデジャネイロ | ミュルーズ | サンクトペテルブルク |
| \(α\) | 0.752 | 0.43 | 0.42 |
| \(A_1\) | 0.18 | 1.15 | 1.37 |
| 係数 | Austria pine |
| \(A\) | 0.25 |
| \(B\) | 0.39 |
| \(C\) | 0.25 |
| \(E\) | 0 |
| \(G\) | 0.05 |
【森林:地上パス】 【上空から到来する電波(スラントパス)】
| 記号 | パラメータ説明 [単位] | 適用範囲 |
| \(A_1\) | 最大減衰を計算するための係数[dB] | |
| \(d\) | 樹木帯の経路長[m] | |
| \(f\) | 周波数 [GHz] | 0.03GHz~100GHz |
| \(α\) | 最大減衰を計算するための係数 | |
| \(\gamma\) | 減衰係数[dB/m] |
| 記号 | パラメータ説明 [単位] | 適用範囲 |
| \(f\) | 周波数[MHz] | 30MHz~100,000MHz |
| \(θ\) | 仰角 [degree] | |
| \(d\) | 森林の通過距離[m] |
計算例
【上空から到来する電波(スラントパス)】

参照
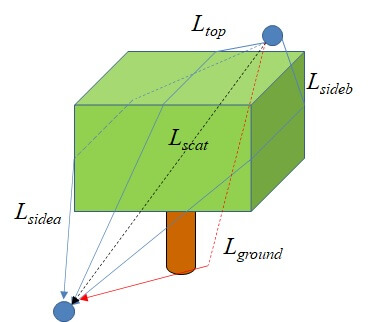
[1] ITU-R P.833-10, “Attenuation in vegetation”, 2021.【参考】1本の木による減衰
1本の木による減衰については、ITU-R P.833-10に詳細に記載されている。下図のように木の頂上を通過するパス(\(L_{top}\))、木の両側を通過するパス(\(L_{sidea},L_{sideb}\))、木の下の地面で反射して到来するパス(\(L_{ground}\))、木の中を通過するパス(\(L_{scat}\))のすべてを考慮して次式で表せる。
\(
L_{total} =-10 \log_{10}\left[10^{\frac{-L_{sidea}}{10}}+10^{\frac{-L_{sideb}}{10}}+10^{\frac{-L_{top}}{10}}+10^{\frac{-L_{ground}}{10}}+10^{\frac{-L_{scat}}{10}}\right]
\tag{4}
\)
各要素については、ITU-R P.833-10及びITU-R P.526, ITU-R P.1238に詳述されているので参照されたい。