Recently, the research and development of quantum computers have been growing rapidly all over the world; they have also been significantly increasing in importance in Japan. This has definitely been caused by a huge amount of knowledge on quantum computers accumulated over many years through the constant challenges of researchers to pursue the truth. Quantum computers are those which explicitly utilize the effect of quantum mechanics, which is completely different in principle from current computers (a.k.a, classical computers), to achieve extremely fast computation that classical computers cannot. For such computation, it is crucially important to discover novel algorithms to derive tremendous computation power from the hardware of quantum computers as well as to develop novel hardware technologies. As quantum computers cannot solve all problems faster than classical computers, the challenge is to first identify the problems that are possible to solve faster with quantum computers, and then to find concrete procedures (i.e., algorithms) for solving those problems with quantum computers.
The recipients have been tackling these challenges and have achieved outstanding results from the following two aspects: (1) distributed computing over many quantum computers connected via communication channels [1-5], and (2) computing on a single quantum computer [6-10], which may be a constituent of a distributed computing network. The following are two of their major results:
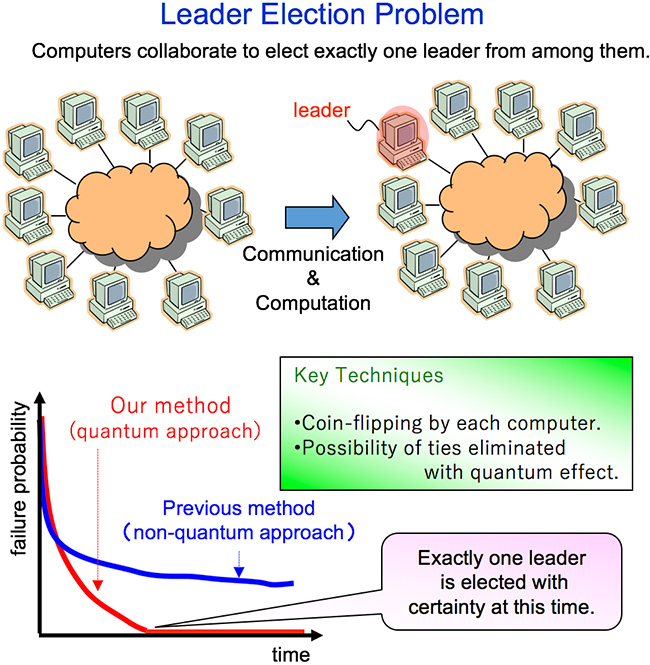
- The leader election problem, a major problem in distributed computing, is impossible to solve deterministically (i.e., without error within any finite time) over classical computers in most general settings. One of the recipients with his collaborators discovered quantum algorithms that solve the problem without error in a bounded time [2] (Fig. 1). This contrasts sharply with all previous works on quantum algorithms, which had focused on how quickly quantum computers can solve problems that classical computers can solve if long computation time is allowed. Thus, the significance of this result is to first present a natural problem and quantum algorithms for it where the problem cannot be solved on classical computers even with an enormous amount of computation and communication.
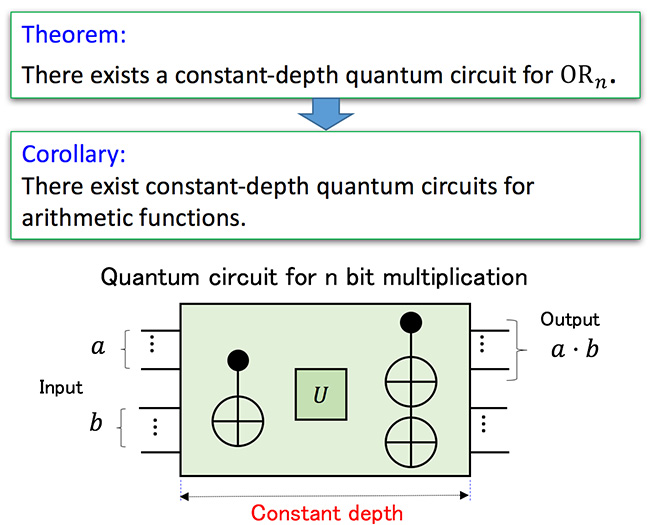
- Arithmetic functions such as addition, subtraction, multiplication and division are basic computing components and thus incorporated in various algorithms, while threshold functions are constituents of artificial neural networks. The recipients devised remarkably fast quantum algorithms in the form of quantum circuits for computing these functions [8] (Fig. 2). The significance is that their quantum circuits can compute the functions in a constant depth independent of the number of input bits. This contrasts strikingly with logic circuits computing the functions, the depth of which inevitably increases depending on the number of input bits. This means that, for a large number of input bits, their algorithm can compute the functions in a very short time, which classical computers cannot achieve. This short computation time could significantly decrease undesirable influences over the quantum computation from environmental noise, against which quantum state is well-known to be fragile.
In conclusion, the recipientsf work has contributed significantly to the foundation of quantum algorithms by embodying the power of quantum computation as concrete quantum algorithms for natural problems, and thus they definitely deserve the IEICE Achievement Award.
Fig.1 Quantum algorithm for the leader election problem
Fig.2 Constant-depth quantum circuits for arithmetic functions
- S. Tani, M. Nakanishi, and S. Yamashita. "Multi-party quantum communication complexity with routed messages." IEICE Transactions on Information and Systems, Vol. E92-D, No. 2, pp. 191-199, 2009.
- S. Tani, H. Kobayashi and K. Matsumoto. "Exact quantum algorithms for the leader election problem."@ACM Transactions on Computation Theory, 4(1):Article 1, 2012.
- S. Tani. "Compression of view on anonymous networks - folded view -." IEEE Transactions on Parallel and Distributed Systems, Vol. 23, No. 2, pp. 255-262, 2012.
- H. Kobayashi, K. Matsumoto and S. Tani. "Simpler Exact Leader Election via Quantum Reduction." Chicago Journal of Theoretical Computer Science, vol. 2014, article 10, 2014.
- S. Tani. "A Fast Exact Quantum Algorithm for Solitude Verification." Quantum Information & Computation, vol.17, no. 1&2, pp. 15-40, 2017.
- Y. Takahashi, S. Tani, and N. Kunihiro. "Quantum addition circuits and unbounded fan-out." Quantum Information and Computation, Vol. 10, No. 9&10, pp. 872-890, 2010.
- Y. Takahashi. "Computational Power of Quantum Circuits with a Small Number of Steps."The Journal of IEICE, Vol. 97 No. 12, pp. 1110-1114, 2014.
- Y. Takahashi and S. Tani. "Collapse of the hierarchy of constant-depth exact quantum circuits." Computational Complexity, Vol. 25, No. 4, pp. 849-881, 2016.
- Y. Takahashi, S. Tani, T. Yamazaki, and K. Tanaka. "Commuting Quantum Circuits with Few Outputs are Unlikely to be Classically Simulatable." Quantum Information & Computation, vol. 16 , no. 3&4, pp. 251-270, 2016.
- Y. Takahashi and S. Tani. "Power of uninitialized qubits in shallow quantum circuits." Proc. 35th Intf Symp. Theoretical Aspects of Computer Science (STACS 2018), pp. 57:1-57:13, 2018.